1、波动是物质的一种运动形式
▲ 机械波 — 机械振动在弹性介质中的传播过程
如:声波、水波等
(应用如:超声仪、测桩仪)
▲ 电磁波 — 电磁振荡引起的变化的电场与磁场在空间的传播
如:无线电波、紫外线、光线等
(如:钢筋磁感仪、雷达)
2、声波是机械波
▲ 次声波 0~20Hz
▲ 可闻声波 20~20kHz
▲ 超声波 20kHz~1010 Hz ( 砼超声 :20kHz~250kHz)
▲ 特超声波 > 1010 Hz
3、声波的产生与传播: 声波是质点振动的传播过程,产生并传播声波的条件是:
▲要有作机械振动的波(声)源,如声带发出声音、超声发射换能器发出超声波
▲要有传播振动的介质,如空气、水、混凝土,但真空中不能传播机械波
4、振动:物体在一定位置附近重复运动
▲振动位移μ μ=Asinωt
▲振动速度v v=![]() =Aωcosωt
=Aωcosωt
▲振动加速度a a=![]() =-Aω2sinωt
=-Aω2sinωt
A-振幅,离开平衡位置的最大位移
![]() -角频率
-角频率 ![]()
5、波的类型
①最简单的波是纵波和横波
▲纵波(P波)— 质点振动方向与波的传播方向一致,如声波
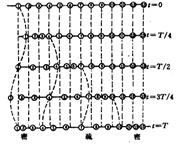 纵波可以在固体、液体、气体中传播
纵波可以在固体、液体、气体中传播
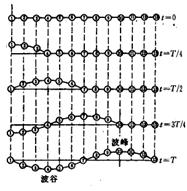
▲横波(S波)— 质点振动方向与波的传播方向垂直
横波只能在固体中传播
 |
|||
 |
|||
②纵波、横波迭加产生其它类型的波
▲表面波(R波)- 纵向振动与横向振动迭加形成椭园振动,沿介质表面传播
表面波只能在固体中传播
 |
6、波的形式
①声波在无限大且各向同性介质中向各方向传播
▲波线 - 传播的方向
▲波前 - 介质中质点振动传播到达的各点的轨迹
▲波阵面 - 介质中质点振动同相位的所有质点的连线(或称轨迹)
②按波阵面分
▲平面波 - 波阵面是平面,振源是无限大平面
▲球面波 - 波阵面是球面,振源是点源
▲柱面波 - 波阵面是同轴园柱面,振源是无限长园柱
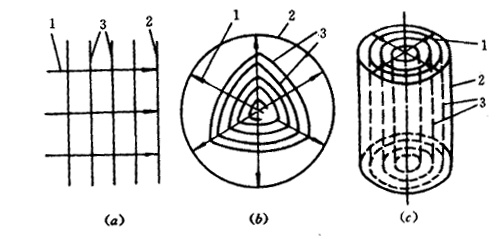 |
(a) 平面波;(b)球面波;(c)柱面波
1-波线;2-波前;3-波阵面
7、基本物理量
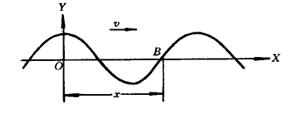
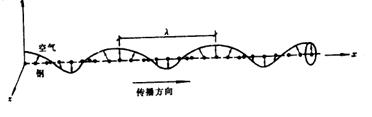
▲周期T - 质点完成一次振动的时间,单位:秒
▲波长λ - 在周期T内波传播的距离,单位:米
▲频率f - 每秒振动的次数,单位:1/秒
▲速度V - 每秒传播的距离,单位:米/秒
基本物理量之间的关系:
![]()
例:V=4000m/s f=50kHz ![]() =80mm
=80mm
二、声速-质点振动传播的速度
1、无限体中的声速
无限体的边界条件:D >2λ (D:横向尺寸、λ:波长)
▲纵波声速VP=![]()
▲横波声速VS=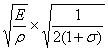 =
=![]()
![]()
▲面波声速VR=![]() Vs
Vs
( E:弹性模量 ![]() :密度
:密度 ![]() :泊桑比 G:切变弹性模量)
:泊桑比 G:切变弹性模量)
纵波声速VP>横波声速VS>面波声速VR
砼中: VP=(1.62~1.87)VS ( 当σ=0.25时 VP=1.73VS)
VP=(1.81~2.08)VR
VR=0.9VS
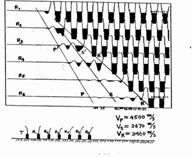

纵波P、横波S、面波R的时序关系 实测的纵波、横波、面波
2、不同几何尺寸介质的纵波声速
▲无限体中的声速(无限体的几何条件:与声线相垂直尺寸大于2倍波长)
![]()
▲薄板介质中的声速(薄板的几何条件:板厚<<![]() ;长x宽Y方向的尺寸>>板厚z)
;长x宽Y方向的尺寸>>板厚z)
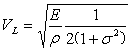 |
▲细长杆(一维杆)声速(细长杆的几何条件:横向尺寸<<![]() ;轴向尺寸>>横向尺寸)
;轴向尺寸>>横向尺寸)
无限体中的声速VP>薄板介质声速VL>细长杆(一维杆)声速VB
![]()
例:砼中: VP ≈ 4500m/s
VL ≈ 4368m/s
VO ≈ 4280m/s
混凝土的σ=0.2~0.23,以锤击作振源时反射波法所测混凝土声速(一维杆的纵波声速)比超声波法所测混凝土声速要低5%~7%
三、声波在声界面的反射与折射(透射)
1、声阻抗率Z:在数值上是密度和声速的乘积,对于一定频率的声波,声阻抗率只取决于介质特性,故也称之为介质的特性阻抗
![]()
混凝土特性阻抗Z=108×104g/cm2.s
2、声界面:指声阻抗率Z不同的介质的界面
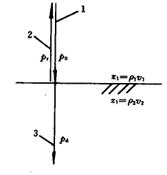 3、垂直入射
3、垂直入射
![]() 声压反射率
声压反射率
![]() 声压透射率
声压透射率
垂直入射:1-入射波;2-反射波;3-透射波
Z1=Z2 相同介质 全透射 R=0,D=1
![]()
![]() Z1《Z2 声疏 声密, 如空气 砼,几乎全反射, R ≈1 D≈0
Z1《Z2 声疏 声密, 如空气 砼,几乎全反射, R ≈1 D≈0
![]()
![]() Z1 》Z2 声密 声疏, 如砼 水,几乎全反射(反射波反相), R≈ -1 D≈0
Z1 》Z2 声密 声疏, 如砼 水,几乎全反射(反射波反相), R≈ -1 D≈0
4、斜入射
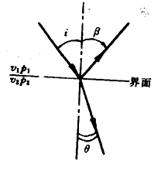
反射定律 ![]() 入射角等于反射角
入射角等于反射角
![]() 折射定律
折射定律
在流体(气体、液体)界面,介质中只有单一的纵波
5、在固体介质的声界面声波将发生方向,角度及波型的变化
一种波(纵波)入射到固体界面时,不仅波方向发生变化,而且波型也发生变化,分离为反射纵波、反射横波、折射纵波、折射横波。各类波的传播方向各不相同,符合反射定律和折射定律
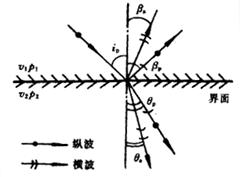 |
6、第一临界角![]() :若入射波是纵波,且
:若入射波是纵波,且![]() (声疏 →声密),则:折射角
(声疏 →声密),则:折射角![]() >入射角
>入射角![]() 当折射角
当折射角![]() =900时的入射角
=900时的入射角![]() 称为第一临界角
称为第一临界角![]()
若纵波入射角>第一临界角,第二种介质中没有折射纵波,只有折射横波,这是产生横波的一种方法
四、声波的绕射
在声阻抗不连续的介质中,声波在传播中会发生声波的绕射
当介质中出现声阻抗差异较大的障碍物和裂缝,空洞及低声阻抗的异物时声波会发生绕射现象
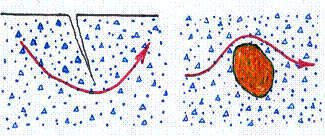
五、声波的散射
不均匀介质,例如混凝土中的骨料、缺陷、掺杂物等,会发生声波的散射
散射只在波长入与粗骨料的粒径d相近时发生,波长(λ)≈骨料粒径(d)
散射会使声传播过程中发生能量损失
由此决定了混凝土超声检测所使用的频率一般要低于200KHz。频率高,能量损失大
六、声波的衰减
声波在传播过程中振幅随传播距离的增大而逐渐减少的现象称为衰减,在超声检测中用首波波幅值的相对变化描述声波的衰减程度
1、产生衰减的原因
▲吸收衰减: 传播中质点间的摩擦使声能转化为热能造成吸收衰减
▲散射衰减: 传播中多次反射、折射,波型转换造成散射衰减
▲扩散衰减: 传播中波束扩散使能量分散造成扩散衰减
2、衰减系数,衰减与频率的关系
平面波:A=Am e-αl; 球面波:A=(1/l )Ame-αl (式中l为声传播距离)
衰减系数![]() :
:
吸收衰减系数 ![]() 正比于
正比于![]()
散射衰减系数 ![]() 正比于
正比于![]()
总的衰减系数 ![]()
a、b、c是由介质性质和散射物特性所决定的比例系数
总体来说,衰减系数是频率的函数,频率越高衰减越大
![]() 3、衰减的度量(波幅的度量):分贝
3、衰减的度量(波幅的度量):分贝
![]() 分贝数=
分贝数=
分贝是用对数表示同一种物理量(接收波声压与标准声压)的相对大小,分贝为无量纲量
相对固定幅度a0 信号幅度a,用分贝表示为幅度A
a=2 a0 a的幅度值
a=1/2 a0 a的幅度值
![]()
a=10 a0 a的幅度值
![]()
a=100 a0 a的幅度值
a=1000 a0 a的幅度值
七、混凝土声学特性
1、 声速与混凝土物性关系
▲由声速可以计算出混凝土的动弹性力学参数:
泊松比μ
弹性模量E
, 剪切模量G
▲声速与混凝土密实度,强度存在相关性:
当声波传播到有缺陷的部位,由于声阻抗变化,声波会产生折射、反射以及绕射现象,使声线拉长,声时加大,视声速下降
2、波幅即衰减系数与混凝土物性关系
致密、强度高的混凝土波幅衰减少
强度低或存在缺陷的混凝土波幅衰减大
3、频率与混凝土物性关系
砼中应用的超声脉冲波是复频波,含有多种频率成份,最主要的频率为主频
在传播过程中高频成份容易衰减掉,使主频向低频侧漂移(频移),主频率变低
混凝土质量差,存在缺陷时接收信号的频移较大,主频率明显变低
